3.1 - La Géodésie ?

La géodésie est la science qui étudie la forme et les dimensions de la Terre, en tenant compte de son champ de pesanteur. La surface de la Terre est très irrégulière et complexe et on peut la modéliser de différentes manières. La sphère est le modèle le plus simple mais n’est pas très fidèle.

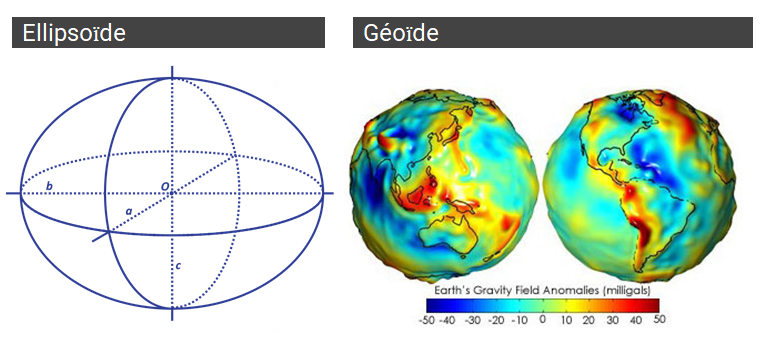
L’ellipsoïde, une sphère aplatit l’est déjà plus et reste assez simple à modéliser. Il se définit généralement par ses demi-axes et son centre. Il existe une infinité d’ellipsoïdes représentant la Terre de manière plus ou moins fidèle au niveau local ou global. Par exemple on peut avoir un ellipsoïde qui représente fidèlement l’Europe.

Enfin, on peut aussi modéliser la Terre grâce à un géoïde. Il s’agit d’une surface perpendiculaire en tout point à la direction de la gravité (fil à plomb). C’est une sorte de sphère cabossée. La représentation est exacte mais lourde à utiliser. Cette représentation est unique.

Figure 3.1 : Ellipsoïde et Géoïde (source : Wikimédia Common)

3.2 - Système de coordonnées

Les coordonnées peuvent être exprimées en degrés, en mètres... et dans des référentiels différents. Un même point aura des coordonnées différentes selon le système de coordonnées utilisé.

Un système de coordonnées est un système utilisé pour mesurer des coordonnées. Il en existe de très nombreux, nous verrons cela dans la suite de ce chapitre dans Qgis. Les principaux à connaître sont :

• WGS84 : le système le plus courant au niveau international mis en place en 1984.
• RGF93 : le système officiel français.
• ED50 : un système mis en place à l’échelle européenne.
• NTF : ancien système local français, abandonné aujourd’hui, mais on peut encore trouver des données utilisant ce système.

Selon le système de coordonnées choisit, un point n’aura pas les mêmes coordonnées. La problématique reste que ces systèmes sont en trois dimensions alors que ce que l’on souhaite pour faire une carte, c’est quelque chose en deux dimensions.

3.3 - Projection

Le principe est de projeter des données 3D (la Terre n'en déplaise à certains n'étant pas plate !) sur une surface plane. Il y aura donc forcément des déformations à l'image d'une peau d'orange qu'on écraserait, et qui se déchire.

On appelle projection cartographique le système de correspondance entre les coordonnées géographiques (latitudes et longitudes) et les points du plan de projection aussi appelés les coordonnées projetés. Ces nouvelles coordonnées sont donc en deux dimensions et sont souvent mesurées en mètres. Une projection permet donc :

• de représenter sur une surface plane une partie d'un modèle ellipsoïdal;
• d’obtenir des valeurs métriques plus facilement exploitables que les valeurs angulaires de latitude et longitude;
• de rendre plus facile une évaluation des distances.

Pour réaliser une projection, on essaye d’envelopper le globe terrestre par une forme que l’on sait dérouler par exemple un cylindre ou un cône. Cela amène à catégoriser les projections en trois grands groupes : les projections cylindriques, les projections coniques, et les projections azimutales. Pour les projections cylindriques, l’ellipsoïde est projeté sur un cylindre qui enroule le globe. Ce cylindre est ensuite déroulé pour obtenir la projection. Pour les projections coniques, l’ellipsoïde est projeté sur un cône qui enroule le globe. Là aussi il est déroulé pour obtenir la carte. Enfin pour la projection azimutale, l’ellipsoïde est projeté sur un plan tangent en un point.

Figure 3.2 : Trois grands types de projection

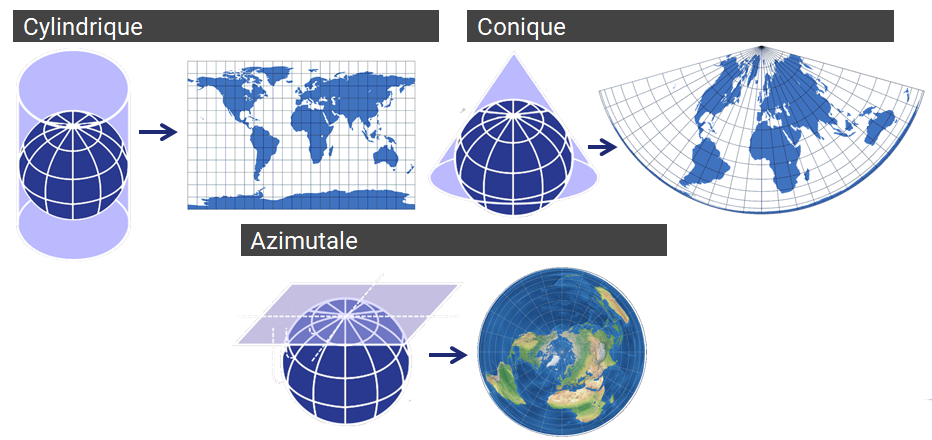
Les projections peuvent aussi être classées selon leurs propriétés. On distingue ainsi les projections équivalentes, qui conservent les surfaces ; les projections conformes qui conservent les angles et les projections aphylactiques qui conservent les distances sur les méridiens. Une projection ne peut être à la fois conforme et équivalente. Voici quelques exemples de projections :

• La projection Mercator, qui conserve les angles mais où les surfaces sont de plus en plus déformées à mesure que l'on s’éloigne des pôles.
• La projection cylindrique équivalente de Peters, qui donne vision juste des proportions des surfaces des continents
• La projection conique conforme Lambert, qui est utilisée pour représenter seulement une partie du globe. Dans ce cas les déformations sont minimisées pour la France. C'est donc une des projections les plus utilisée en France.

Figure 3.3 : Quelques exemples de projection

Pour aller plus loin ...

Il existe une multitude d’autres types de projections. Si vous souhaitez aller plus loin sur ce sujet, cet article de blog recense de nombreux outils pour appréhender la notion de projection.

3.4 - Système de coordonnées de référence (SCR)

Le système de coordonnées de référence (SCR) associe un système de coordonnées et une projection. Il en exsite de très nombreux.

Sur QGis il faut distinguer le SCR du projet du SCR des couches. Par défaut, QGis assignera au projet le SCR de la première couche ajoutée à l'espace graphique. Dans la mesure du possible le logiciel tentera de reprojeter toutes les autres couches ajoutées dans ce SCR.

Cependant, il est plus commode de travailler avec des couches qui sont dès le départ toutes dans le même SCR.

Exercice 3.1 : Déterminer le système de coordonnées de référence d'un projet et d'une couche

1/ Télécharger les bases de données.

2/ Les décompresser et les ajouter à un projet QGis en commençant par la couche contenant les routes du département d'Indre et Loire.

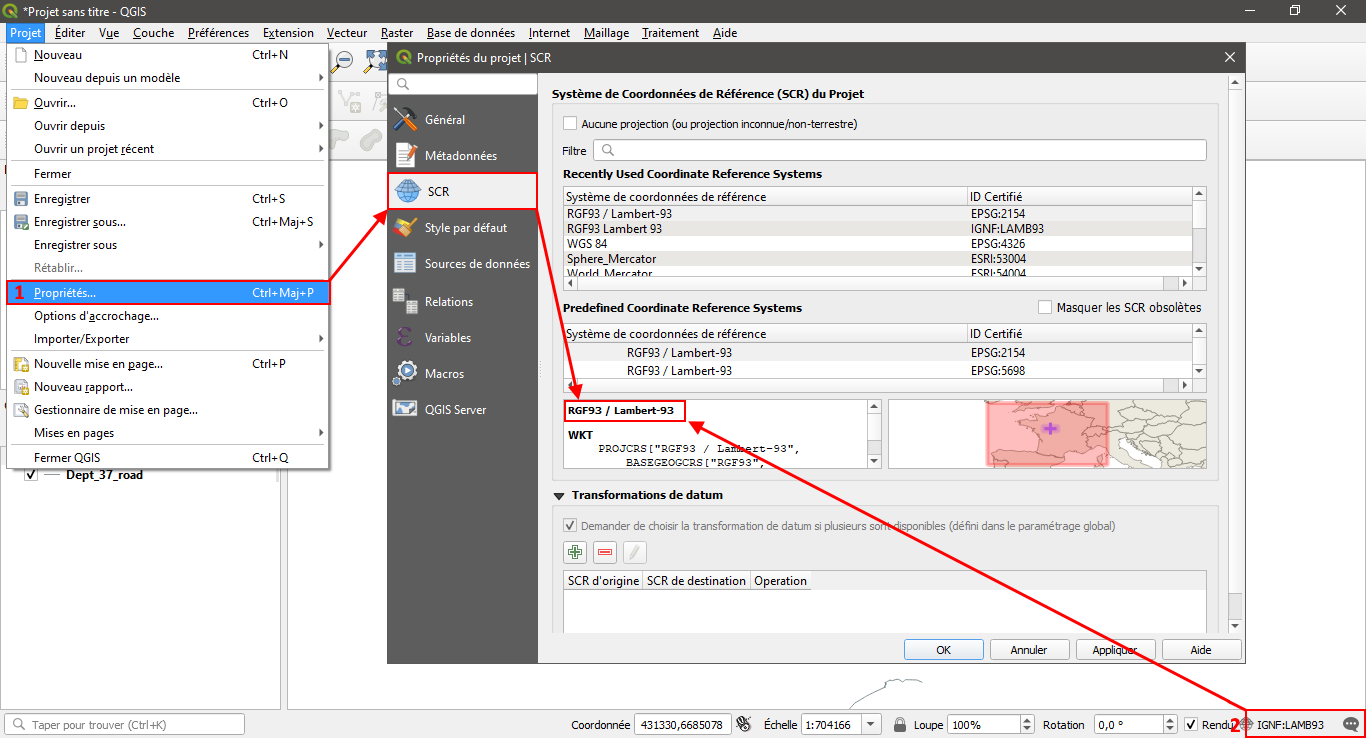
3/ Aller dans «Projet>Propriétés…>SCR »(1) ou cliquer dans le coin inférieur droit (2) et déterminer le SCR du projet.

Figure 3.4 : Déterminer le SCR du projet.

4/ Pour chacune des deux couches, dans la fenêtre « Couches » faire un clic droit sur une des couches vecteur chargée puis « Propriétés > Source ». Déterminer le SCR de chacune des couches.

Figure 3.5 : Déterminer le SCR d'une couche.

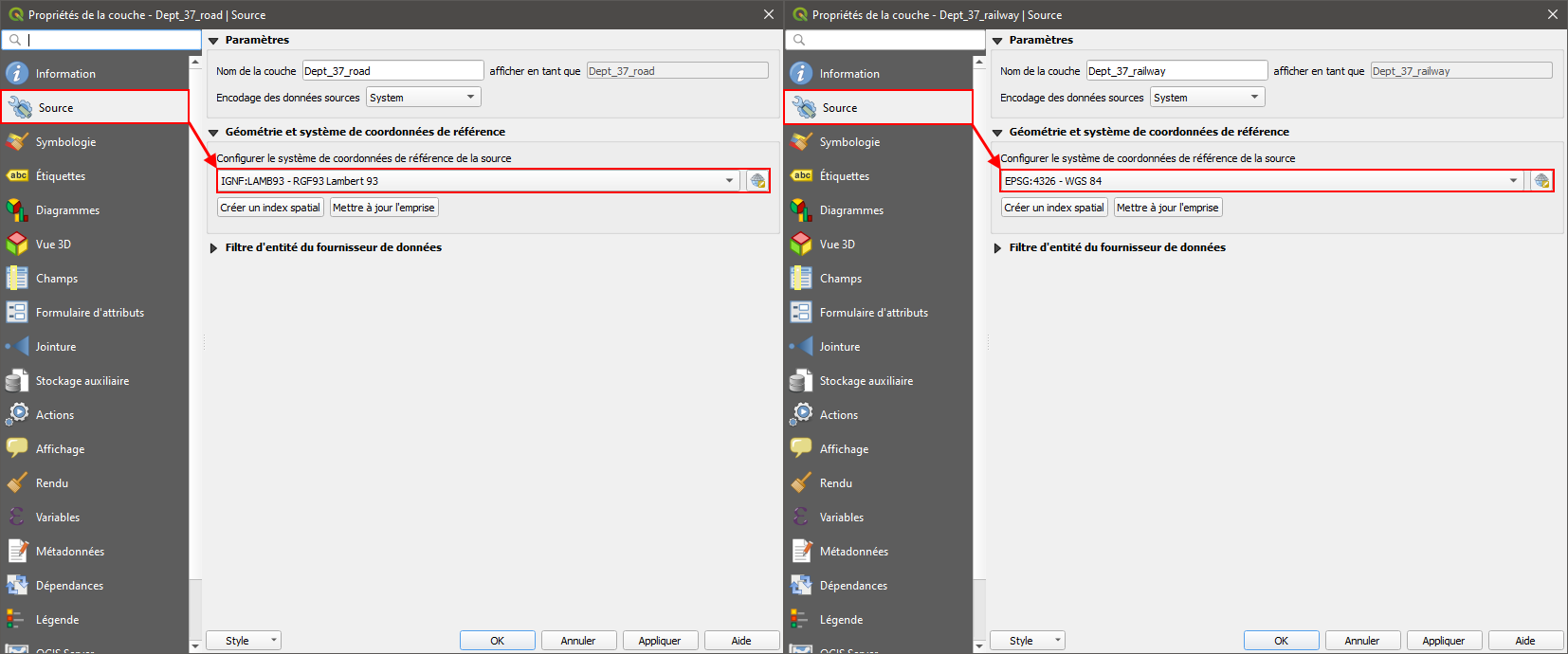
Vous devez normalement constater que les SCR des deux couches ne sont pas les mêmes. Pourtant, celles-ci s'affichent "bien" dans l'espace graphique : QGis a reprojeté la couche du réseau ferré dans le SCR de la couche du réseau routier.

Exercice 3.2 : Corriger la projection d'une couche de données vecteurs

Dans cet exercice, l'objectif est de corriger la projection d'une couche de données vecteurs (ou la projeter dans un système de coordonnées différent). Les couches à considérer sont celles chargées lors de l'exercice 3.1.

1/ Dans la fenêtre « Couches » faire un clic droit sur la couche Dept_37_railway puis « Exporter>Sauvegarder les entités sous…».

Figure 3.6 : Modifier le SCR d'une couche.

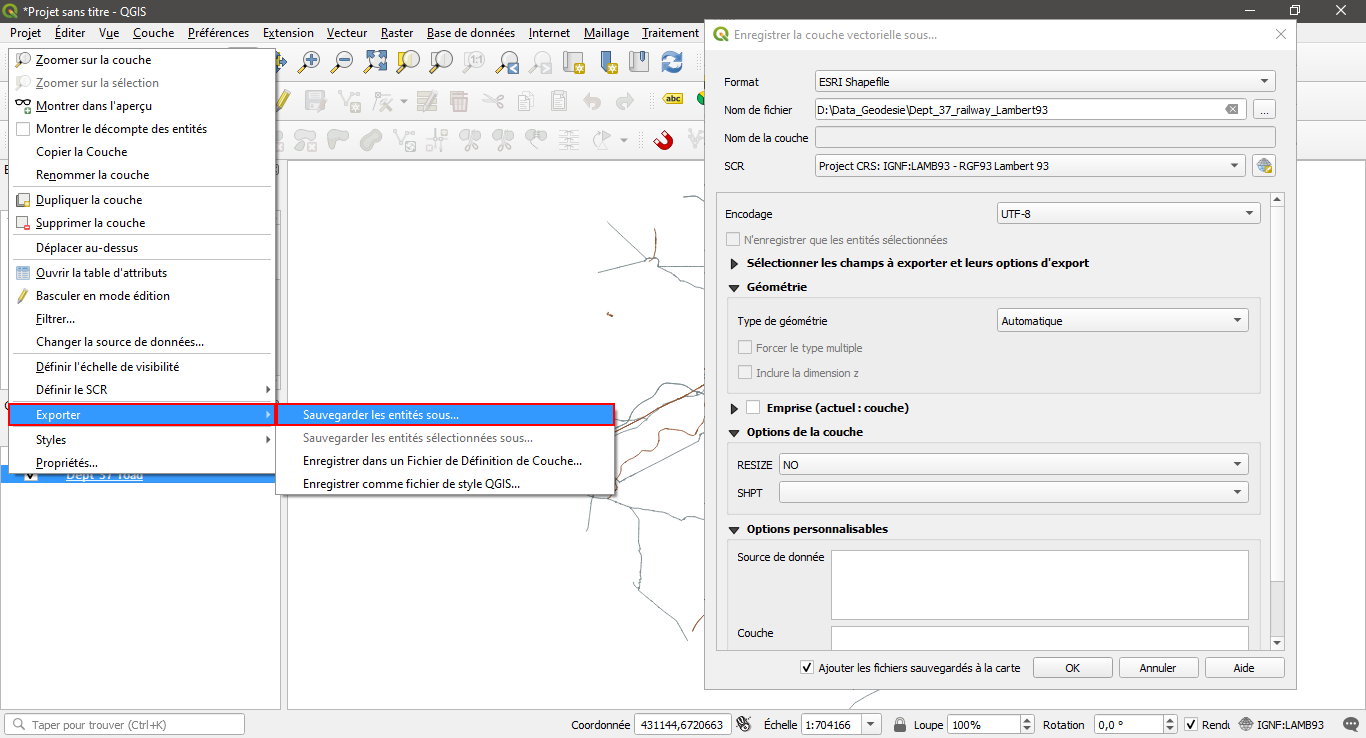
2/ Donner un nom au fichier et définir le SCR en sélectionnant « SCR du Projet : … ». En enregistrant ce nouveau fichier, une nouvelle couche est créée : celle-ci contient les données de la couche Dept_37_railway dans le système de coordonnées de la couche Dept_37_routes.